








John Bayerl, 3/24/2025, 7:15p









John Bayerl, 3/24/2025, 7:15p
[I’m posting this “Remembrance” that I wrote last summer after the death of my neighbor and friend, Al Lubran. I revisited this piece today and was especially taken with Al’s deathbed premonition of the dire effects on our government if DT were elected. Unfortunately, his premonition is proving to be all too accurate.]
Al Lubran was a new friend who lived just around the corner from my spouse Andrea and me in our retirement community – The Village At Rockville (TVAR). He moved in a few weeks after we did in March 2022. We knew that Al had moved from Colorado Springs, where he was a longtime resident. Al was a rather private person, and it took some time before we got to know him better.
We shared with Al a love for live classical music, and we frequently ran into him at the Strathmore and other concert venues. Al also attended a lot of plays around town and often had good tips for upcoming concerts and other local cultural events. He regularly rode the Metro downtown to the Kennedy Center and other venues, even with his portable oxygen device for the last few months.
Al was an avid crossword puzzle fan – a passion he shared with Andrea and another neighbor on our floor. The New York Times Magazine weekly puzzle was one they always shared – making copies of it for one another and comparing their results afterwards. Al also regularly played bridge and poker at TVAR. He was active on TVAR’s Travel Committee and initiated some bus excursions to local concerts.
Al was a master of humor, regaling many of us here with his funny stories and puns. He had a keen appreciation for political satire, and filled our email inboxes with videos and cartoons, all with a decidedly anti-Trump bent. Al was also a regular attendee of TVAR’s monthly meeting of our Democratic Club.
We got to know Al more deeply after he came over one afternoon recently to tell us that his health was quite shaky and that he wouldn’t be around for long. We had been noticing him with a portable oxygen unit from time to time, but that soon became a constant companion. Al said that he had a fatal condition called pulmonary fibrosis and that his pulmonologist advised that he get his affairs in order and contact hospice. We were taken assured him that we were available to help in any way.
We knew just a few elements of Al’s biography – that he was from Steubenville, OH, that he had served in the military and then worked for the Federal government for most of his career. We also learned that he had been an avid skier and world traveler, passions which he had shared with his wife Donna, who died in 2018. Al met Donna in Colorado, and they lived in Colorado Springs for decades. Al had moved to the DC area because he had two younger brothers (twins) who lived here. His doctor had recommended that he move somewhere with a lower elevation to facilitate his compromised breathing. Al celebrated the fact that he’d had two good years living at TVAR before his lungs started giving out.
I visited Al in his apartment a few times after he shared his dire news with us. He was remarkably sanguine about dying, accepting his fate with grace and dignity. He wanted to remain in his home to the end and contracted with the Jewish Social Services Agency for in-home hospice care. His two brothers, Bernie and Bob, supported him to the end, along with his devoted friend, Carol Stein. He died at home on the morning of June 18.
I learned from Al’s brothers a bit more about the arc of his life. He had gone to college at the Case Institute of Technology in Cleveland, OH and then enlisted in the Air Force, where he rose to the rank of Captain. Al was proud of his military service in Turkey and stateside. He then went to work for IBM but left in order to move to the place he loved, Colorado Springs. He then went to work for the Federal government as a contracting officer based in Denver. He spent the rest of his career as a devoted public servant, serving in a number of Federal agencies. He spoke proudly of the fact that he had saved American taxpayers millions of dollars with his keen procurement strategies.
My last visit with Al was the most memorable. He shared how afraid he was feeling. Given his acute breathing disability, I assumed he meant he was afraid of dying. But no, he waved that off, and said he was really afraid that all his hard work as a Federal civil servant would come to naught if Donald Trump was elected to a second term. I was taken by his pride in his accomplishments and his deep appreciation for the established system of government he had worked for in both Republican and Democratic administrations.
May Al’s spirit rest in peace. May his fear for the future of our country be alleviated.
John Bayerl, 6/26/2024
On January 2, 2025, I posted a piece called “My Introduction to Sacred Geometry.”
My next foray into “sacred geometry” began with the fish-shaped form created by the intersection of two circles. After drawing the first circle, a second circle with the same radius as the first is drawn, using a point on the first circle’s circumference as the center. The result is shown below.
Vesica Pisces

The shaded area in the center is central to Euclid’s classic geometry. The fish-like shape was also incorporated as a symbol of Christ in the early Christian church. This lens-like form is called the “vesica pisces”, or “bladder of a fish”.
The basic form of the “vesica pisces” can be extended into a complex, repeating form called the “flower of life”. My own drawing of the “flower of life” is given below. I won’t go into the exact methodology for constructing it here, but I will say it took many days of trial-and-error drawings.

Vesica Pisces and Euclidian Geometry
The vesica pisces form was used by Euclid to illustrate some important mathematical relationships.
First, a rectangle is drawn using the vertical diameters of both circles as the two sides. Then, the top and bottom of the rectangle are drawn by connecting the intersection points of the vertical diameters on the two circles. The resulting rectangle has some interesting properties.

The Pythagorean theorem is central to Euclidian geometry. The theorem makes use of a universal property of any right-triangle (i.e., any triangle that has a “right” angle of 90 degrees). In such a triangle, the longest side is called the hypotenuse. The theorem has to do with the relative lengths of the three sides of a right triangle. It says that the length of the hypotenuse, squared, is equal to the squares of the lengths of the other two sides.
The Pythagorean theorem can be used with the rectangle around the “vesica pisces” as shown in the figure above. First a line is drawn connecting opposite corners of the rectangle. This creates a right-triangle in which we already know the lengths of the two shorter sides.
We can define the radius of each circle as a length of 1 unit. Thus, we can easily see that the vertical lines of the rectangle are exactly 2 units tall (the length of two radii). Similarly, we can see that the top and bottom lines of the rectangle are the same length as the radius: 1 unit.
Using the Pythagorean theorem, we can calculate the length of the slanted line, the hypotenuse, as the square root of the squares of 1 and 2. The square of 1 (1X1) is 1 and the square of 2 (2X2) is 4. So, the length of the slanted line is the square-root of 5. You can use a calculator to estimate the square root of 5 as: 2.2360679775…
This is regarded as an irrational number – one whose succession of decimal digits follows no known pattern. The Greeks were intrigued by irrational numbers like this. The square root of 5 became an important number in the calculation of another important irrational number, Theta.
The value of Theta is calculated as half the value of the square root of 5, plus another half unit. Half the value of the square root of 5 is: 1.1180339887… Add .5 units to this and you get: 1.618033987… which is the value of Theta.
The Golden Rectangle
Theta is the value that defines what was known to the Greeks as the Golden Rectangle. A golden rectangle is defined as one in which the lengths of the sides are in proportion to the value of Theta.
The next figure shows a golden rectangle that is divided into a square and another rectangle. The sides of the square can be identified as “a”, and the length of the whole rectangle can be given as: “a+b”.

In a golden rectangle, the following equation always holds:
a / b = (a + b) / a
This equation always yields the exact value of the irrational number Theta.
A Golden Rectangle Drawn from the Vesica Pisces
The rectangle enclosing the vesica piscis is NOT a golden rectangle. Its width is 1 radius unit, and its height is 2 such units. The proportion is simply 2 to 1, or 2.
But the hypotenuse of the right triangle drawn in Figure 2 can be used to construct a golden rectangle. Recall that the value of Theta can be expressed as the square root of 5, divided by 2, and adding .5. Looking at Figure 2, it’s easy to see that the length of the hypotenuse, the square root of 5, is exactly bisected by the midline of the circles. Therefore, the length of half of the hypotenuse is the square root of 5, divided by 2. The additional .5 units can be drawn as half the length of the radius (1 unit). Knowing that this length represents the value of Theta, we can simply add one more radius unit and we have the known value of A and B.
Once this is known, it’s easy to draw the square with each side of length Theta, and an additional rectangle whose length is 1. The combination as a whole yields a golden rectangle. And the secondary rectangle contained within is also a golden rectangle, as shown below.

The Golden Rectangle became the design model for the Greek Parthenon and many other of the classical structures of the Greco-Roman era. Many Renaissance artists, most notably Leonardo da Vinci, made extensive use of the Golden Rectangle in their paintings and architecture.
The Fibonacci Sequence and Theta
The value of Theta can also be calculated by using the arithmetic sequence known as the Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…. The sequence starts with 0 and 1, with each succeeding value being the sum of the previous two. Divide each number in the sequence by its predecessor and the value will approximate Theta, getting closer and closer to it as the sequence continues. For example, 89/55 = 1.61818 and 144/89 = 1.61797.
Pursuing my interest in Sacred Geometry has opened in me a deeper curiosity and respect for some of the universal design principles used in western art and architecture.
John Bayerl, 3/11/2025
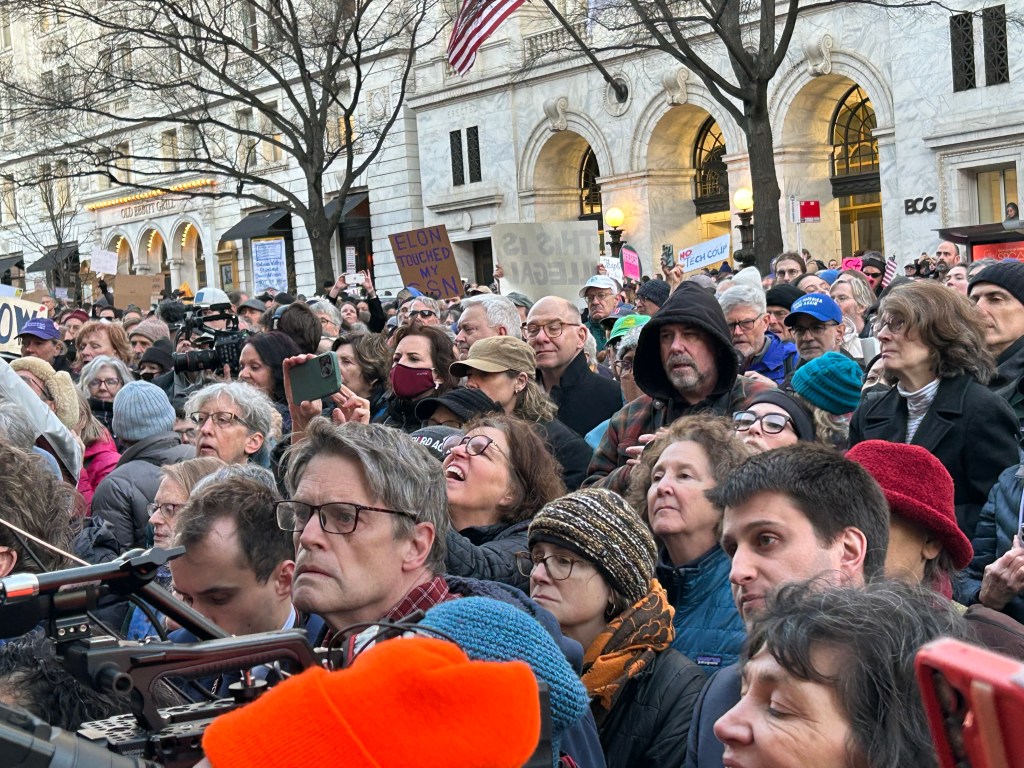
I just returned from a rousing resistance rally at the U. S. Treasury building in downtown Washington. The rally was organized by the MoveOn and the Indivisible organizations after Elon Musk’s egregious invasion and takeover of the U.S. Treasury and its sensitive computer systems over the weekend.
A crowd of thousands thronged the sidewalk and street in front of the building on 15th Street, NW. A contingent of Democratic U.S. Congresspersons, Senators and Representatives, many of them on Government Oversight Committees, had been turned away from entering the building
The rally featured over a dozen members of Congress as well as leading spokespersons for MoveOn and Indivisible. My fellow Indivisible member and friend Raj Gupta joined me for the Metro ride downtown. We arrived early enough to get prime standing positions just behind the official video cameras of the event.
We were both inspired by the energy and enthusiasm of the speakers and the crowd. The speakers’ list included Senators Elizabeth Warren (MA), Chris Van Hollen (MD), Chris Murphy (CT), Ron Wyden (OR), Richard Blumenthal (CT), and Democratic Minority Leader Chuck Shumer (NY). From the House side were Rep. Maxine Waters (CA), Ayanna Pressley (MA), Jaime Raskin (MD) and a number of others.
Ezra Levin of Indivisible gave a rousing speech, forcefully calling on the Senators to shut the Senate down in protest of the outright coup at the Treasury. Rahna Epting, the Executive Director of MoveOn, deftly facilitated the event after giving her own stirring call to action.
I took some photos and have posted a few of them below.
John Bayerl, 2/4/2025









I read of an intriguing idea recently: that a list of the books we read is a kind of autobiography reflecting our deepest interests. For what it’s worth, I decided to compile my list from last year and post it here. I was surprised to find that I had equal numbers of fiction and non-fiction. The seven titles with a preceding asterisk are ones I read as part of a Bayerl Family book group that is entering its ninth year.
I’ve already posted blog reviews of three of last year’s books, as follows:
“Killers of the Flower Moon” as Book and Film, book written by David Gann, film directed by Martin Scorsese, 1/22/2024
“Anything Is Possible” by Elizabeth Strout, 5/27/2024
What’s My Excuse?, a review of Viktor Frankl’s “Yes to Life in Spite of Everything”, 6/24/2024
NON-FICTION
1 *Killers of the Flower Moon, David Gann
2. The Gospel According to James Baldwin, Greg Garrett
3. Uncle Tom’s Journey from Maryland to Canada – The Life of Josiah Henson, Edna M. Troiano
4. Yes to Life, (translation of Viktor Frankl’s essays called “In Spite of Everything”). Daniel Coleman (ed,)
5. Proof of Heaven, Eben Alexander
6. *Democracy Awakening, Heather Cox Richardson
7. A Year to Live, Stephen Levine
8. * Beautiful Country, Quian Julie Wang
9. A Passionate Mind in Relentless Pursuit – the Vision of Mary McLeod Bethune, Noline Rooks
10. In Search of Stones,M. Scott Peck
11. The Road He Travelled – The Revealing Biography of M. Scott Peck, Arthur Jones
FICTION
1. *American Savior, Roland Merullo
2. *The River We Remember, William Kent Krueger
3. Anything Is Possible, Elizabeth Strout
4. *Goodnight, Irene, Luis Alberto Urea
5. Olive Kitteridge, Elizabeth Strout
6. The Little Liar, Mitch Albom
7. The Next Person You Meet in Heaven, Mitch Albom
8. *Trust, Hernan Diaz
9. Olive, Again, Elizabeth Strout
10. *The Storm Beyond the Tide, Jonathan Cullen
11. Foregone, Russell Banks
John Bayerl, 1/26/2025

I just returned from the People’s March on Washington, an energetic affair of some tens of thousands who marched from three different sites in downtown DC to the grounds of the Lincoln Memorial for a lively rally.
Andrea and I had attended the memorable Woman’s March of January, 2017, which was a different order of magnitude, with many hundreds pf thousands showing up in DC to protest Trump’s first inauguration.
The Trump 2.0 protest was every bit as creative, energized, and lively as 8 years ago, but at a much lower volume. I took the Metro downtown from Rockville by myself this time, Andrea being down with a bug. Instead of marching, I walked directly to the Lincoln Memorial grounds from Foggy Botton Metro station, a commute I knew well from my 15 year career at the GW Medical Center there.
Some people from the rally, laden with their political signs and creative attire, were walking back up to Foggy Bottom from the rally already. There was a festive feeling in the air. The marches had started at 10am and I was only arriving at the rally after 1pm.
Being on my own, I was free to follow my nose, allowing me to focus on taking photos with my smart phone once I arrived after about a mile walk down 23rd Street to the Washington Mall. Without the huge crowds of 2017, I was able to relax more and really take in the sights and sounds. Below are some of the photos I took.
John Bayerl, 1/18/2025




















We made our second visit to the OMMA today on a gloriously clear autumn morning. We had visited it a year ago with our friends and hosts, Joan Jacobs and Larry Drake of neighboring Portsmouth, NH. We had fond memories of its Maine seaside locale and the charming village of Ogunquit, widely recognized for its rich arts, crafts, and theater offerings. The museum is on the edge of town fronting a dramatic seascape.
Andrea and I spent much of our time in the outdoor sculpture garden that surrounds the sleek, low to the ground, building. The garden features great natural vistas, as well as a sculpture called “Luna” in the background of the next photo, and many others tastefully arranged to reflect the natural beauty of the setting.


Inside the gallery, there were special showings of two mid-20th century American artists: Russell Cheney and Lee Kramer.
Cheney was a New Englander who lived and worked in Portsmouth, NH and neighboring Kittery and Ogunquit, ME. He painted in a somewhat traditional realist style with great sensitivity to the humanity of his portraits and a poetic rendering of light and space.

Cheney was a gay man who lived quietly with his life partner, the Harvard professor and author F.O. Matthiessen, for decades. He is much celebrated in Ogonquit by the large gay community there who have long lived in peace with their neighbors. The painting below is a self-portrait of Cheney (l.) and Matthiessen.

Lee Kramer is one of the important originators of an abstract movement in late 1930’s America. She was inspired by the Dutch artist Piet Mondrian’s style of precise, geometric abstractions.
Kramer was the spouse of the more celebrated artist Jackson Pollock. Personally, I much prefer her own contained, visually pleasing abstract creations to the wild expressionism of her alcoholic husband.

We took a second stroll into the adjoining sculpture court before driving into town for lunch and a long, energizing walk on the expansive Ogunquit Beach.



Remembering a great time together last Fall.
John Bayerl, 1/16/2025

The term “sacred geometry” has become commonplace in New Age culture. According to Wikipedia, “Sacred geometry ascribes symbolic and sacred meanings to certain geometric shapes and certain geometric proportions.” It is associated with the belief in a “divine geometer/creator” from which the physical universe is unfolding in inherently coherent and orderly ways.
One form of sacred geometry that I’ve been working with for many years is the mandala. It is defined simply as a geometric configuration of symbols. Mandalas are used in many spiritual traditions as a means of focusing attention on the inherent order and beauty of the universe. They can be used as an aid to meditation and for establishing sacred space.
My own work with mandalas has primarily involved adding color to existing mandala forms as presented in adult coloring books. I’ve described this work in detail in two of my previous blog pieces:
Finding Relaxation and Focus in Coloring Mandalas | John’s Blog
More recently, I’ve become interested in generating my own mandala templates using simple geometry. For guidance and inspiration in this process, I’m indebted to the book Islamic Geometric Patterns by Eric Broug. More than an aesthetic study of Islamic graphic motifs evident on many mosques, shrines, and other holy places, Broug’s book is an instructional guide for constructing complex Islamic-inspired designs using simply a ruler, compass, and pencils (ordinary and colored).
First Attempt
The figure below is my first attempt to create a mandala. Its geometry is relatively simple. It starts with drawing a circle with horizontal and vertical lines running through the center point. The circle intersects the vertical line above and below the center point. And the circle intersects the horizontal line to the left and right of the center point. Each of those four intersecting points then becomes the center of another circle of the same radius as the first.

A sixth circle can then be drawn using the four intersection points of the four outer circles. I used the center of the first circle and measured (with a compass) the distance to the four outer circle intersection points. This sixth circle has a larger radius than the other five circles and is concentric with the original circle.
It took me a few attempts to get a satisfying result. After meditating on it for a bit, I decided to color in a four-petal flower pattern that emerges. I also used a red pencil to highlight the circumferences of all six circles. I was pleased with this first foray into creating a mandala.
Flower of Life
My second foray was a bit more challenging. It involves 6 same-sized circles surrounding an interior circle of equal size. I’m not going to go through the geometric steps involved in creating this here. But like the first figure, it uses intersection points created by previous steps to become the center point for the next circle. All the design is done with compass and straight edge, with no linear measurement required. The finished work is shown in the figure below.

I learned later that the basic template of this figure has been used universally since the time of the ancient Egyptians (6,000BC). It is usually referred to as the “Flower of Life”. There are various interpretations of the symbol across cultures, but a common thread is that it represents “the interconnectedness of all things, the cycle of life, and universal creation”.
This symbol also provides the basis for drawing a perfect hexagon in the center of the central circle.
Concentric Hexagon Mandala
Using what I learned from creating the “Flower of Life”, I was able to easily construct a pattern of 5 concentric hexagons. It involved simply using a compass to draw four concentric circles around the central circle. Then the directional lines used to create the first internal hexagram are extended outward to intersect the concentric circles. The six intersection points on the circumference of each circle become the six points of the hexagon. I added a little color to highlight its mandala character.
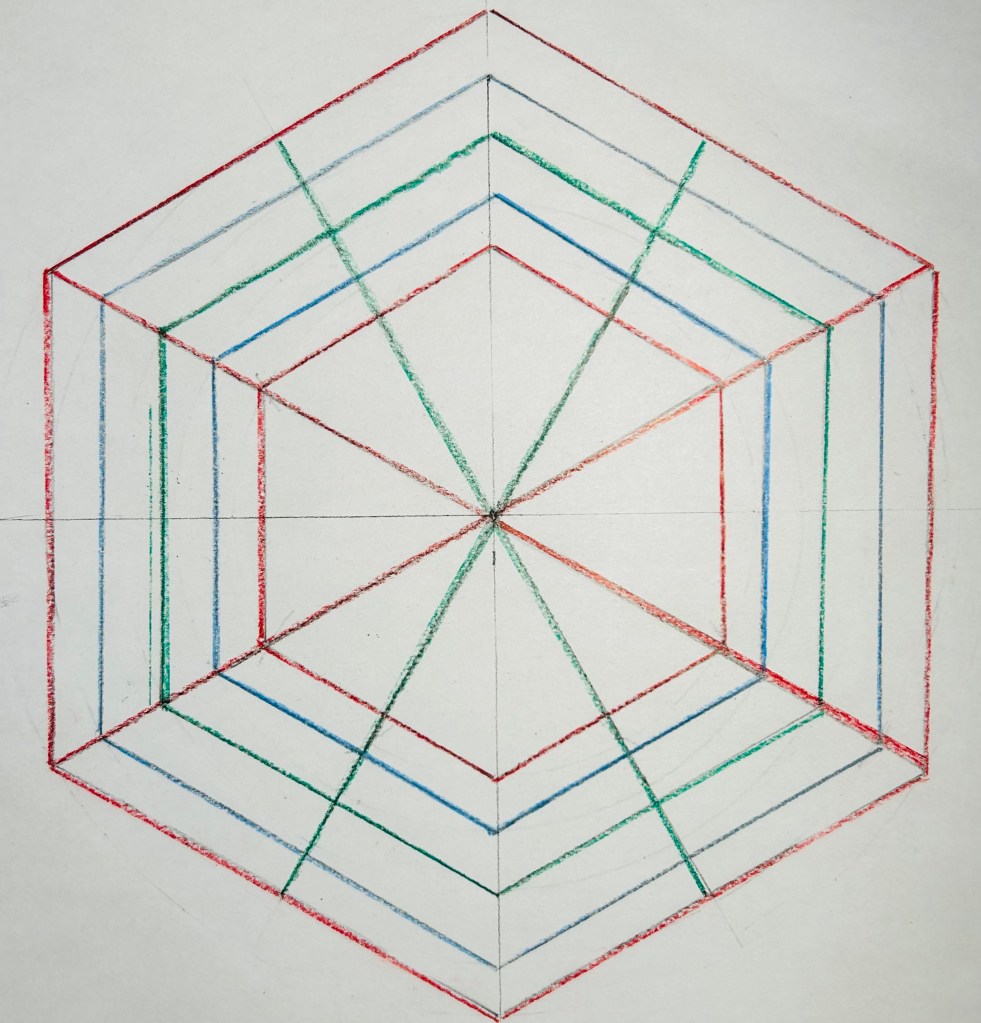
The Great Mosque of Cordoba design template
The first real world example of an Islamic geometric pattern that I explored is based on the next complex figure.

The figure’s central motif is an 8-pointed star. The basis of the design is a circle within a square. Horizontal and vertical lines are drawn through the center of the circle, and then diagonal lines are drawn connecting the opposite corners of the square. The intersection points of the four lines crossing the circle become the points of connection for the rest of the pattern. Once the pattern is complete, some of the construction lines can be erased, yielding the following:

Tessellation
Eric Broug teaches that many of the ornate patterns of design used in the world-famous Great Mosque of Cordoba are simple repetitions of the figure given above. This repetitive process is called tessellation. The formal definition of the term is: “an arrangement of shapes closely fitted together, especially of polygons in a repeated pattern without gaps or overlapping.”
Per Mr. Broug’s suggestion, I made 9 photocopies of the figure above and assembled them together to witness the effect, shown below.

As you can see, the repetition of the original figure yields more interesting and complex patterns. Of course, the actual rendition of this in the Cordoba mosque is much more ornate.
I’m obviously still a novice at this, but I wanted to share my initial enthusiasm at discovering the fascinating realm of sacred geometry.
To be continued…
John Bayerl, 1/1/2025







Georges Braque, Still Life



